A Riemann Sum estimates the area under a curve using rectangles. While this technique is not exact, it is an important tool that you can use if you are unable to differentiate or integrate an equation. 

study guide for Riemann Sum explanation and practice

So imagine you are given this equation: f(x) = x^2. Your interval is [0,5] and n = 5. For the purposes of simplicity, I am going to demonstrate a Left Riemann Sum.

1. Understand the information that the question gives you.

Equation: f(x) = x^2
Interval: [a,b] and in the case of this problem [1,5] - these are the parameters for the section under the curve that you are estimating
N: n=4 - this number determines how many rectangles you are splitting the section under the curve into. (Note: More rectangles = more precision, but also means more work)

2. Find Δx: the width of each of your rectangles.

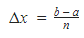
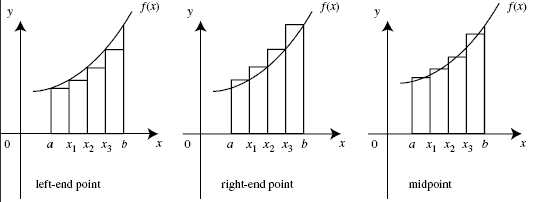
3. Find the height of each rectangle: where the top left (for a Left Riemann Sum) corner of each rectangles meets the curve.

(**If you were to take a Right Riemann Sum you would use the top right corner of each rectangle and if you were to use a Midpoint Riemann Sum the height would be where the middle of each rectangle hit the curve)

Our heights for this specific problem would be 1, 4, 9, and 16

4. Find the area of each rectangle, and add them together.

(1)(1) + (1)(4) + (1)(9) + (1)(16) = 30 

^In simplest terms, this equation will help you solve any Riemann Sum. Note that all the steps are the same for Right Riemann Sums except for #3. Just remember to use the top left corner of your rectangles for each Left Riemann Sum and the top right corner for each Right Riemann Sum. 

AP Calculus AB/BC

"The limit does not exist." In unit 1 of AP Calc AB/BC, we cover everything you need to know about limits and continuity: limit notation, estimating and calculating limits, L'Hopital's Rule, squeeze theorem, theories of continuity, infinite limits, limits at infinity, and the intermediate value theorem. 

Unit 1 – Limits & Continuity

In unit 2 of AP Calc AB/BC, we introduce the derivative—definitions of the derivative, derivative rules (power rule, quotient rule, product rule, and trig rules), and differentiability of a function. With these resources, you will become a master of differentiation!

Unit 2 – Fundamentals of Differentiation

In unit 3 of AP Calc AB/BC, we dive deeper into derviatives! We will cover the derivatives of composite, implicit, and inverse functions, including inverse trigonometric functions. We'll delve into higher order derivatives, chain rule, and how to select a procedure to calculate derivatives. 

Unit 3 – Composite, Implicit, & Inverse Functions

In unit 4 of AP Calc AB/BC, we'll cover derivatives as they relate to position/velocity/acceleration, rates of change, and related rates. You'll learn the contextual meaning of derivatives, approximating values using linearization, and finding limits with L'Hopital's Rule. You'll understand the real-life applications of differentiation!

Unit 4 – Contextual Applications of Differentiation

In unit 5 of AP Calc AB/BC, we talk about mean value theorem, Rolle's theorem, extreme value theorem, global & local extrema, functions increasing & decreasing, first derivative test, concavity, second derivative test, and optimization problems. You'll be ready to analyze all types of graphs using the fundamentals of differentiation!

Unit 5 – Analytical Applications of Differentiation

In unit 6 of AP Calc AB/BC, we wil cover accumulation change with definite integrals, Riemann sums, the Fundamental Theorem of Calculus, u-substitution, antiderivatives, indefinite integrals, and properties of integrals, integration by parts, and partial fraction decomposition. You'll understand the fundamentals of integration and its applications!

Unit 6 – Integration & Accumulation of Change

In unit 7 of AP Calc AB/BC, we delve into differential equations, slope fields, Euler's method, finding particular solutions using initial conditions & separation of variables, and logistic models for exponential growth and decay. With these resources, you'll develop a deeper understanding of differential equations as mathematical models.

Unit 7 – Differential Equations

In unit 8 of AP Calc, we dive into integration as it relates to the average value of a function, net changes, particle motion (position/velocity/acceleration), areas between curves, and volumes (with cross sections, disc method, & washer method). You'll develop a solid understanding of integration and its applications in real life!

Unit 8 – Applications of Integration

In unit 9 of AP Calc BC, we review parametric equations, arc lengths, polar coordinates, vector-valued functions, and areas under polar curves. With these resources, you'll ace the AP Calc BC exam!

Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)

Let's learn about series in unit 10 of AP Calc BC. We cover infinite sequences and series, including all the divergence and convergence tests: nth term test, integral test, comparison tests, alternating series tests, and Taylor polynomials. 

Unit 10 – Infinite Sequences & Series (BC Only)

Frequently Asked Questions

Check out these resources for the multiple choice section of the AP Calculus exam. With helpful videos reviewing multiple choice questions, and the best strategies that will help. Covering all sorts of problems and all the topics of AP Calculus, these resources will give you a better understanding of what to expect on the AP Calculus exam.

Multiple Choice Questions (MCQ)

Learn about the structure of the free response questions on the AP Calculus exam. With helpful resources, practice problems and reviews of previous FRQs you will feel comfortable with all of the different types of FRQs. And learn about strategies to ensure that you know how to approach each FRQ no matter what topic it covers. 

Free Response Questions (FRQ)

Exam Review 2020

Make sure to check out this question and answer section for AP Calculus! These resources will answer all the questions you have, and will help you prepare for your exam through trivia games and review sessions. 

Q & A sessions

Get a complete overview of the AP Calculus exam to help prepare for the test. Get a refresh on all the units with helpful guides, review sheets and videos, as well as helpful tips and tricks to prepare you for your exam. 

Big Reviews: Finals & Exam Prep

AP Cram Sessions 2021

Live Cram Sessions 2020

What will you learn? 🤔

Unit 1 Overview: Limits and Continuity

Limits

Introducing Calculus: Can Change Occur at An Instant?

Discontinuities

Jump Discontinuity ↔

Point Discontinuity 🕳

Essential Discontinuity ♾️

Removable Discontinuity 🚫

Exploring Types of Discontinuities

How to Determine Continuity at a Point

Examples

Defining Continuity at a Point

Confirming Continuity Over an Open Interval

Confirming Continuity Over a Closed Interval 

Confirming Continuity over an Interval

How to Remove Discontinuities

Removing Discontinuities

Connecting Infinite Limits and Vertical Asymptotes

Limits at Infinity

Objectives:

Essential Knowledge:

Looking Further

Summary

Answers and Review for Multiple Choice Practice on Limits and Continuity

What can we help you do now?

Multiple Choice Practice for Limits and Continuity

Multiple Choice Questions

Intermediate Value Theorem (IVT)

Overview:

Examples:

     Summary

Working with the Intermediate Value Theorem (IVT Calc)

Defining Limits and Using Limit Notation

Estimating a Limit Value: Step by Step 

Estimating Limit Values from Graphs

Example Problem ❓

Estimating Limit Values from Tables

Example Problem: Using the Sum Rule to Determine a Limit ➕

Example Problem: Using the Constant Multiple Rule to Determine a Limit ➡

Example Problem: Using the Product Rule to Determine a Limit ✖️

Example Problem: Using the Exponent/Power Rule to Determine a Limit 💥

Determining Limits Using Algebraic Properties of Limits

Example Problem: Determining a Limit Using Factoring 

Example Problem: Determining a Limit Using Alternate Forms of Trigonometric Functions 

Determining Limits Using Algebraic Manipulation

Selecting Procedures for Determining Limits

The Squeeze Theorem 

Determining Limits Using the Squeeze Theorem

Connecting Multiple Representations of Limits

What is a derivative? 

Computing Derivatives

An Introduction to Differentiation ⤴

Unit 2 Overview: Differentiation

What is a Derivative? 🤔

Defining Average and Instantaneous Rates of Change at a Point

Derivatives of Special Functions, Continued!


Example Problems:


Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions

Multiple Choice Practice for Differentiation: Definition & Fundamental Properties

Answers and Review for Multiple Choice Practice on Differentiation: Definition & Fundamental Properties


What can we help you do now?

MC Answers and Review

Derivatives Defined

Defining the Derivative of a Function and Using Derivative Notation

Estimating Derivatives

Understanding the Definition of an Estimated Derivative:


Exploring the Estimated Derivative through Different Methods:


Example Problems:

Estimating Derivatives of a Function at a Point

Differentiability and Continuity


Defining Differentiability and Continuity:


Connecting Differentiability and Continuity:


Connecting Differentiability and Continuity: Determining When Derivatives Do and Do Not Exist

The Power Rule

Applying the Power Rule

Derivative Rules

Derivative Rules: Constant, Sum, Difference, and Constant Multiple

Derivatives of Special Functions 💭

Derivatives of cos x, sinx, e^x, and ln x

The Product Rule

The Quotient Rule

Developing Understanding

Building Mathematical Practices

Preparing for the AP Exam

Exam Weighting ⚖

Developing Understanding 🧠

Main Topics and Sections:

Unit 3 Overview: Differentiation: Composite, Implicit, and Inverse Functions

What is the Chain Rule? 🔗

When to Use the Chain Rule 📆

How to Apply the Chain Rule 🤔

Chain Rule Practice 📝

Answers 📝

The Chain Rule

What is Implicit Differentiation?

How to Differentiate Implicitly 🕵

Implicit Differentiation Practice 📝

Implicit Differentiation

What are Inverse Functions? 🙃

How to Differentiate Inverse Functions 🕵

Differentiating Inverse Functions Practice 📝

Differentiating Inverse Functions

What is an Inverse Trigonometric Function? 🤠

How to Differentiate Inverse Trigonometric Functions 🕵

Differentiating Inverse Trigonometric Functions

Calculating Derivatives Practice 📝

Selecting Procedures for Calculating Derivatives

What is a Higher-Order Derivative? 😵

How to Calculate Higher-Order Derivatives 🕵

Calculating Higher-Order Derivatives Practice 📝


Answers 📝

Calculating Higher-Order Derivatives

Multiple Choice Practice for Differentiation: Composite, Implicit & Inverse Functions

Answers and Review for Multiple Choice Practice for
Differentiation: Composite, Implicit & Inverse Functions

🔍 Prerequisite Information 

Unit 4 Overview: Contextual Applications of Differentiation

Review: Implicit Differentiation ✔️

Interpreting the Meaning of the Derivative in Context

Position and Velocity

Acceleration

Straight-Line Motion: Connecting Position, Velocity, and Acceleration

🔍 Examples

📓 Practice

Rates of Change in Applied Contexts other than Motion

What are Related Rates?

The Process 📠

Example Problem:

Draw a Picture

Equation to Relate

Plugging In And Solving

Intro to Related Rates

Special Example: Volume of a Cone 🍦

Solving Related Rates Problems

Linearization

Under and Overestimates

Linearization and Point-Slope

Approximating Values of a Function Using Local Linearity and Linearization

Indeterminate Forms

L'Hopital's Rule

When You Can Use L'Hopitals

Using L'Hopitals Rule for Determining Limits in Indeterminate Forms

Multiple Choice Practice for Differentiation: Contextual Applications of the Differentiation

Answers and Review for Differentiation: Contextual Applications of the Differentiation

How to do a Riemann Sum?

AP Calculus AB/BC ♾️

Riemann Sums

1. Understand the information that the question gives you.

2. Find Δx: the width of each of your rectangles.

3. Find the height of each rectangle: where the top left (for a Left Riemann Sum) corner of each rectangles meets the curve.

4. Find the area of each rectangle, and add them together.

About Us

Resources

Student Wellness

Stay Connected

About Us

Resources

Student Wellness