SAT Math: How Do I __ on my Calculator? 🧮
4 min read•september 11, 2021
SAT 🎓
62 resourcesSee Units
SAT Math: How Do I __ on my Calculator?
Overview
Math will be the third and fourth sections on the SAT:
- 25-minute non calculator section, followed by
- a 55-minute section, where a calculator is allowed. 🖩
→ Each section begins with multiple-choice questions with four answer choices.
→ After the multiple choice questions will be student "grid-in" questions.
→ The reference sheet will be available in ALL sections.
Breakdown of the Two SAT Math Sections:
| Section | Number of Questions | Time ⏱ |
| No Calculator | 15 multiple-choice, 5 grid-in | 25 minutes |
| Calculator | 30 multiple-choice, 8 grid-in (including one Extended Thinking Question) | 55 minutes |
| Total | 58 Questions | 80 Minutes |
A Few Reminders
- Before the test, check this link to make sure your calculator is allowed.
- Before the exam, make sure that you charge your calculator.
- Don’t forget to take your calculator! You cannot borrow or share calculators, and the test site will not provide them.
- Some of the grid-ins will relate to one another on the calculator portion as part of an Extended Thinking question.
Topics Often Tested on the Calculator Section
- Basic operations and negation of values
- Decimals, fractions, percentages
- powers/exponents (square, square root, higher powers)
- Parentheses
- Numerical solver function
- Graphing functions - linear and nonlinear
- Using tables
What You Need To Know
- Be able to do basic calculations (+, -, *, /)
- Work with decimals: change from decimal to fraction and vice versa
- Work with percentages
- Changings signs of numbers (negation)
- Finding square roots
- Squaring numbers
- Raising a value to a power, either using the ^ or the xy buttons
- Graph a given algebraic equation.
- Solve equations by factoring or using other methods (for example, using the zeros of the graph to factor).
- Select a graph that matches a nonlinear equation or an equation that corresponds to a graph.
Sample Problem Section
Calculator section practice problems
General directions for this section you should expect to see:
- The use of a calculator is permitted. But not needed on every problem
- All variables and expressions are real numbers unless otherwise noted.
- Figures are drawn to scale unless told otherwise.
- Assume that the domain of a given function is the set of all real numbers.
1. The following is considered “easy” in difficulty. This requires creating a linear function to represent a real-world scenario.
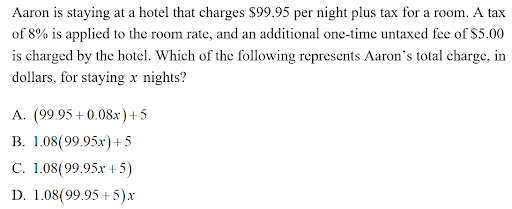
AP college board SAT practice problems
The correct answer is B.
Aaron’s total stay will be the fixed rate of $99.95 plus the tax, which is found by multiplying 0.08*99.95… this per x days, added to the one time charge of$5… combining, this will give (99.95 + 0.08*99.95)*x + 5, which simplifies to choice B.
2. This problem is considered medium-level difficulty. It requires the learner to identify the pattern for an exponential relationship given a real‑world scenario.

AP college board SAT practice problems
The correct answer is D.
The first two choices are linear, so since the question says “the population will DOUBLE…”, which implies an exponential answer, eliminate them. A calculator table could be used to find the function, or the two possible choices could be graphed, and the resulting table would confirm that choice D shows population doubling after a time (x-value) increase of 12.
3. The next question is considered “easy,” requiring the learner to use fractions/decimals (if they choose) to solve an inequality:
If -9/5 < -3x + 1 < -7/4 what is one possible value of 9x - 3?
AP college board SAT practice problems
The correct answer is any value greater than 21/4 (or 5.25) and less than 27/5 (or 5.4).
The calculator could be used in a few ways here--for example, you can change fractions to decimals to start the problem.
Additionally, when dividing by the -3 (necessary to solve for x), the calculator can help ensure that there is no error in sign change.
If the chosen calculator has the nSolve command, this could also help, as well as graphing the inequality pieces to find the intersections (that serve as the solutions).
4. The final calculator question for this section is considered a medium level of difficulty. It requires the learner to build and interpret a real-world problem using conversion for gigabytes and megabytes.

AP college board SAT practice problems
The correct answer is B.
The values in this problem are large enough to warrant the use of the calculator to ensure speed and accuracy of calculations:
1 hour = 3600 seconds.
1 gigabit = 1024 megabits.
3*3600*11 = 118,800 megabits.
Dividing this by 1024 will give 118,800/1024 = 116.015625 gigabits each day.
If each image is 11.2 gigabits, then 116.0156/11.2=10.3585, which is approximately 10 images per day (round down).
Closing
Congratulations! You’ve made it to the end of “SAT Math - How to use the Calculator” prep 🙌 You should have a better understanding of the Math sections for the SAT©, topic highlights, what you will have to be able to do to succeed, as well as have seen some practice questions that put the concepts in action. Good luck studying for the SAT Math section 👏
Helpful Resource Links
- official sample practice questions (all topics) from the AP College Board
Browse Study Guides By Unit
📚Reading
📝Writing and Language
✍️Essay
✏️Frequently Asked Questions

© 2023 Fiveable Inc. All rights reserved.