📚

All Subjects

♾️

AP Calc

👑

Unit 1

1.15 MC Answers and Review

4 min read•december 29, 2021

AP Calculus AB/BC ♾️

279 resources

See Units

Answers and Review for Multiple Choice Practice on Limits and Continuity

Image from Wikimedia Commons

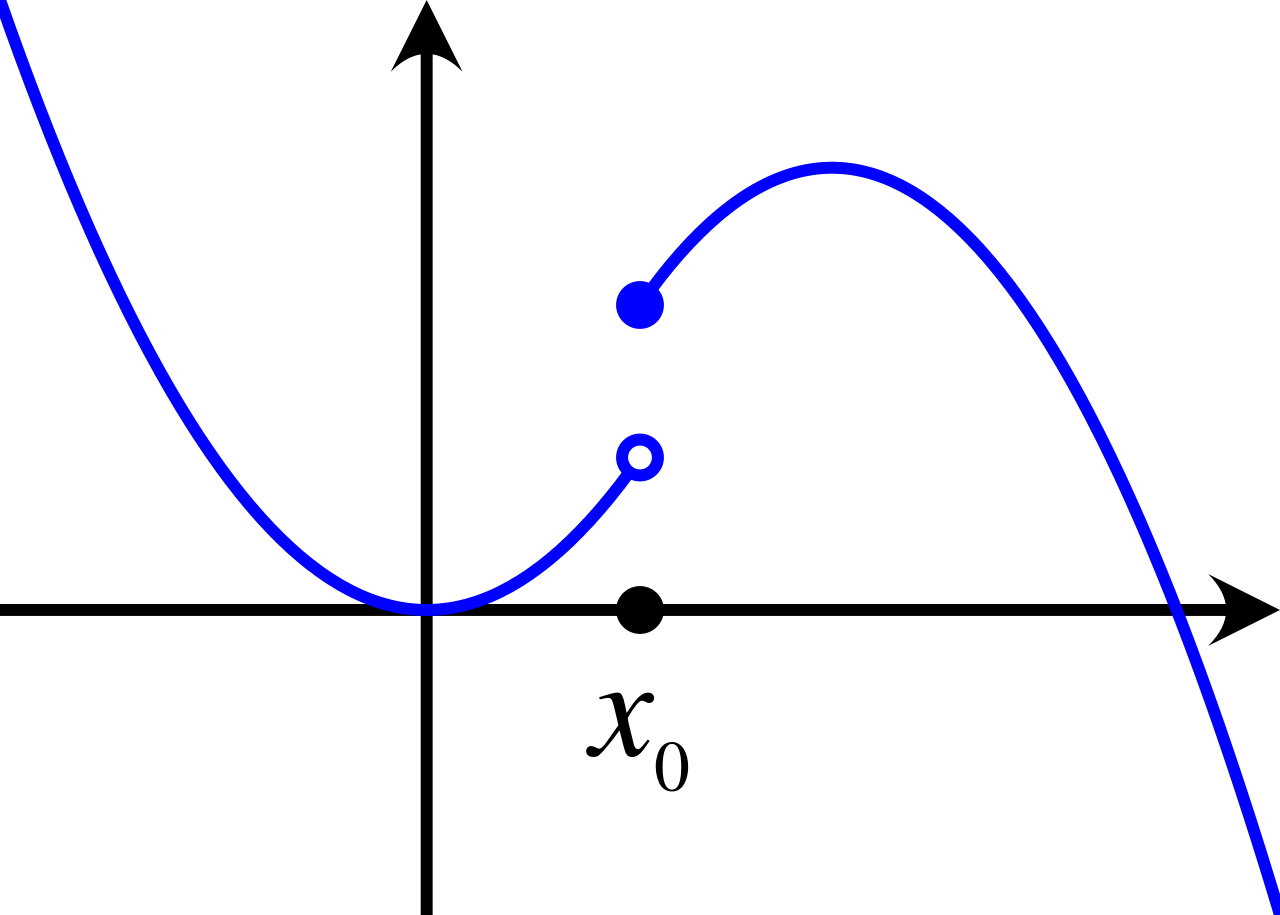
⛔STOP!⛔ Before you look at the answers make sure you gave this practice quiz a try so you can assess your understanding of the concepts covered in unit 1. Click here for the practice questions: AP Calculus Unit 1 Multiple Choice Questions.

Facts about the test: The AP Calculus exam has two sections of multiple choice: 30 questions in 60 minutes with no calculator, and 15 questions in 45 minutes with a calculator.

*The following questions were not written by CollegeBoard and although they cover information outlined in the AP Calculus Course and Exam Description the formatting on the exam may be different.

Explanation: D is correct because For a limit to existence, the limit must be equal on both the left and right side of the value. Therefore, the limit as x approaches 2 does not exist.

📄 Study Unit 1.3: Estimate Limits from Graph

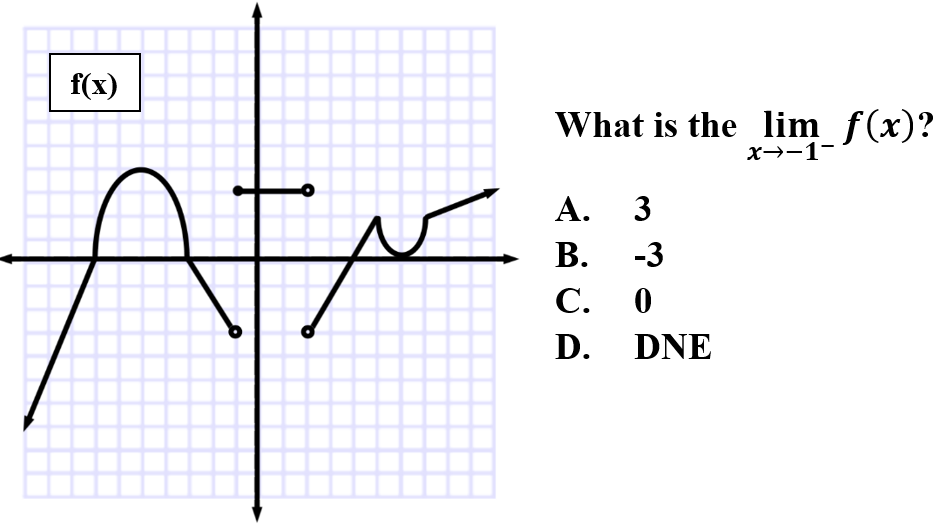
Explanation: B is correct because for one-sided limits, the negative notation as x approaches -1 indicates we are viewing all x < -1. Therefore, as x approaches -1 from the left the limit approaches -3.

🎥 Watch: Graphical Limits

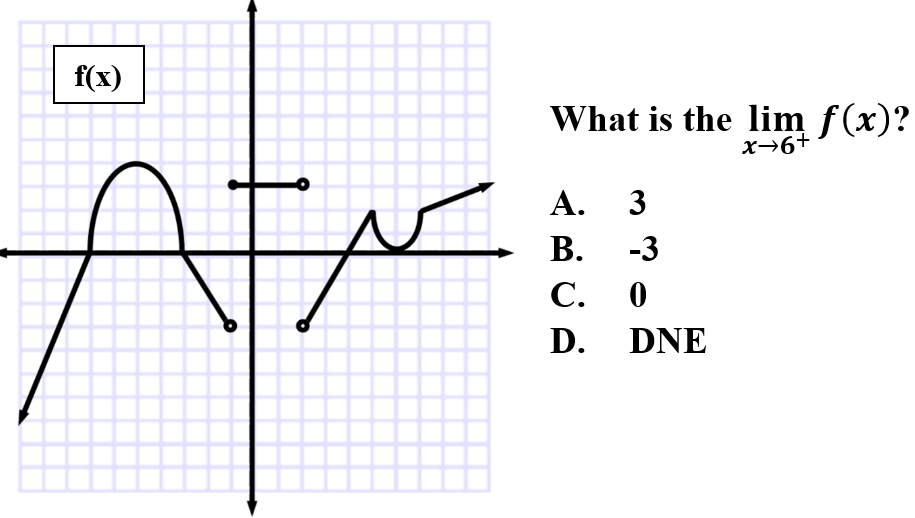
Explanation: C is correct because for one-sided limits, the positive notation as x approaches 6 indicates we are viewing all x > 6. Therefore, as x approaches 6 from the right the limit approaches 0.

🎥 Watch: Graphical Limits

Explanation: A is correct because when you substitute x into the function, it creates the indeterminate form which indicates the function may be able to be simplified. The function can be factored in both the numerator and denominator. Once you can cancel out a factor, you will need to substitute the x in the simplified form.

📄 Read Unit 1.6: Determining Limits Using Algebraic Manipulation

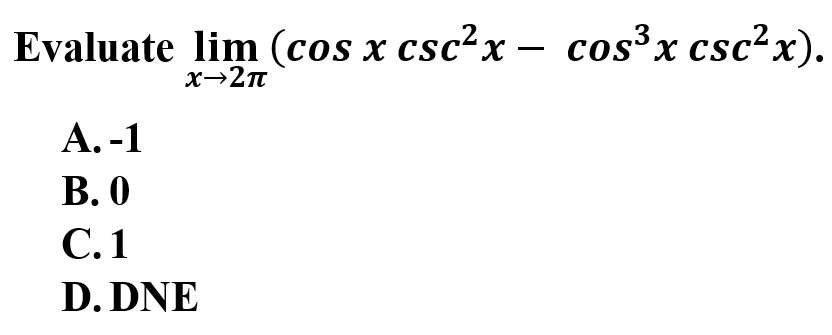
Explanation: C is correct because trigonometric functions often times need to be simplified using trig identities. By direct substitution, the function is undefined. Once you are able to simplify and eliminate a factor, f(x) is 1.

📄 Read Unit 1.6: Determining Limits Using Algebraic Manipulation

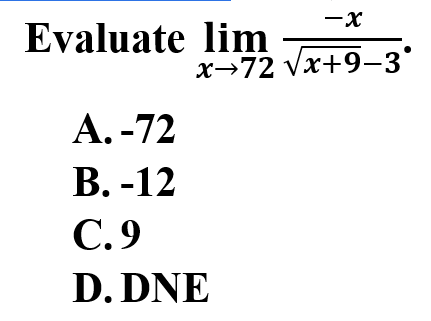
Explanation: B is correct because direct substitution will get you the indeterminate form. Simplification for this function requires eliminating the radical from the denominator. To complete this process, you must rationalize the denominator.

🎥 Watch Algebraic Limits

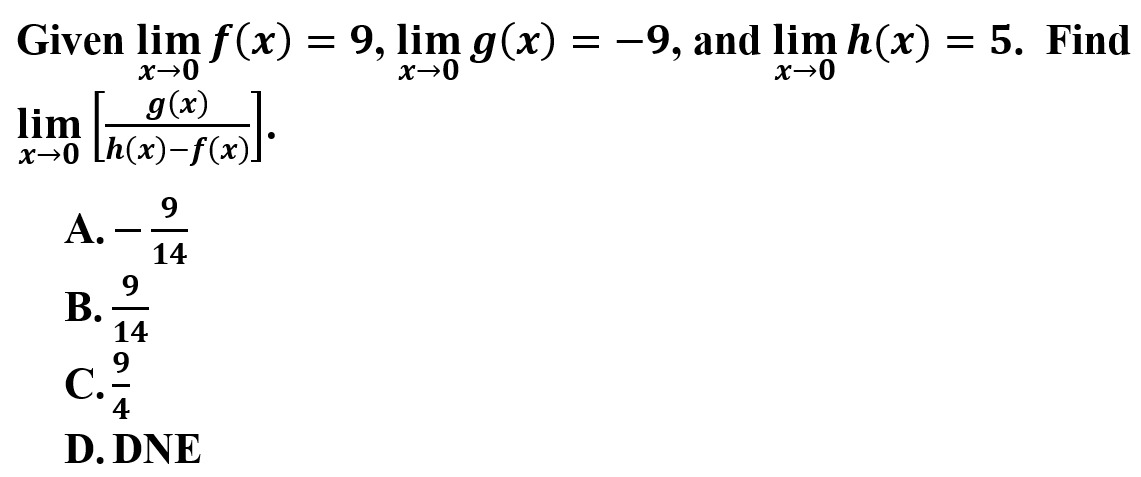
Explanation: C is correct because by the Laws of Limits, values can be substituted into larger functions. Once values are replaced, the limit is found by simplifying basic algebra rules.

📄 Read Unit 1.6: Determining Limits Using Algebraic Manipulation

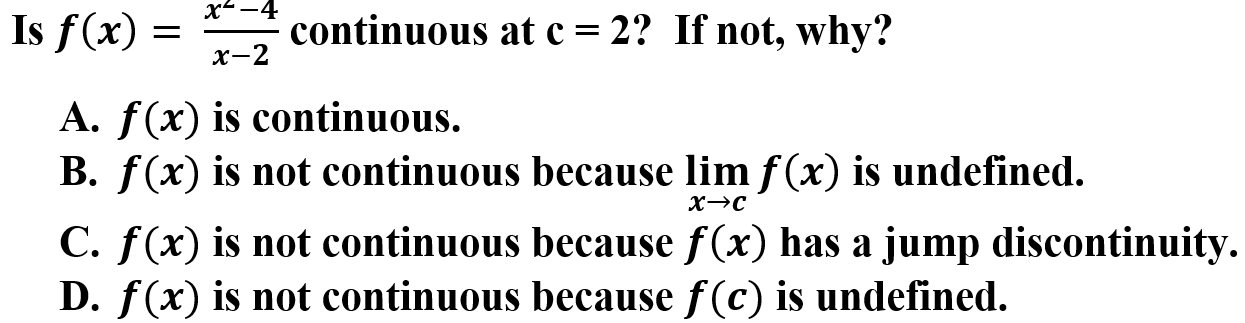
Explanation: D is correct because to be continuous at a point, the limit must exist, f(c) must exist, and the limit must equal to f(c). In this case f(c) does not exist.

📄 Study Unit 1.11: Defining Continuity at a Point

Explanation: B is correct because For the function f(x), f(1) is undefined. Once you plug in x = 1 to both parts of the piece-wise function, the values do not equal. Therefore, there is a jump in continuity of the graph.

📄 Study Unit 1.11: Defining Continuity at a Point

10.

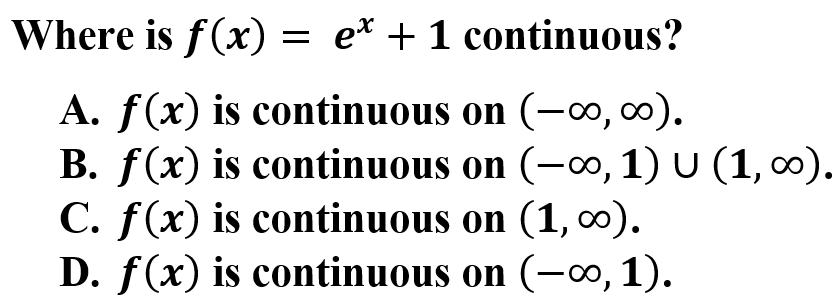
Explanation: A is correct because the function f(x) is an exponential function. Exponential functions are continuous on all x's on their domain.

📄 Study Unit 1.11: Defining Continuity at a Point

11.

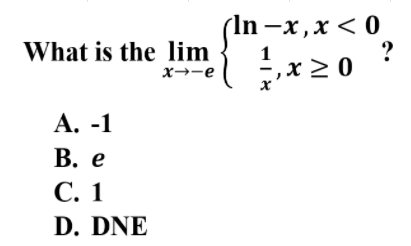
Explanation: B is correct because the limit can be determined by plugging into the piece-wise function. Since the value exist within one side, it does not matter that there is a jump discontinuity at x=0. Therefore, ln -(-e) = 1.

📄 Study Unit 1.10: Exploring Types of Discontinuities

12.

Explanation: D is correct because Since h(x) is continuous and odd nth roots do not have restriction, the composite of these functions yields a continuous functions. To prove continuity, you must prove f(c) exists, the limit exist, and they both are equal.

📄 Study Unit 1.11: Defining Continuity at a Point

13.

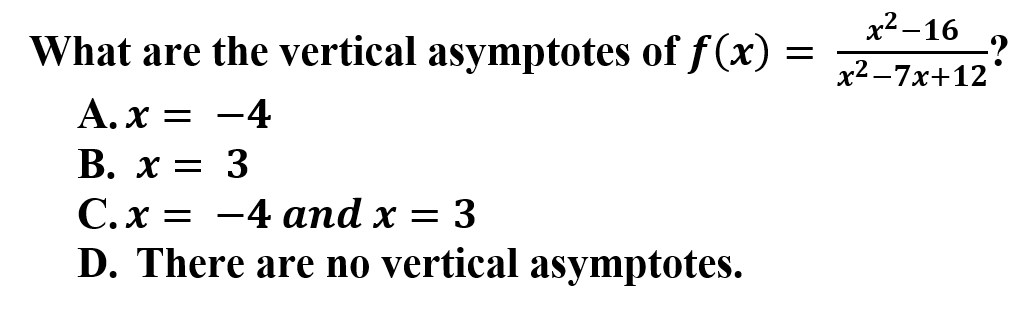
Explanation: B is correct because vertical asymptotes exist because the limits at x = 3 on the right side goes to positive infinity and on the left side goes to negative infinity. There is a hole at x = 4 because when simplifying x - 4 cancels.

📄 Study Unit 1.14: Connecting Infinite Limits and Vertical Asymptotes

14.

Explanation: B is correct because to simplify an absolute value, it must possess a positive and negative version. This yields -1 and 1. The limit in this case wants the left sided limit, so the answer is -1.

🎥 Watch Algebraic Limits

15.

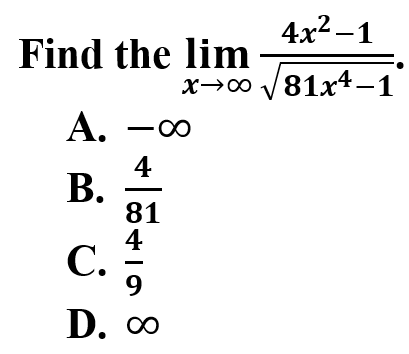
Explanation: C is correct because when locating limits approaching infinity, the process is similar to finding horizontal asymptotes. Both numerator and the denominator have a degree two function after simplifying. Therefore, the numerator is 4 and the denominator is the square root of 81 which is 9.

🎥 Watch: Limits at Infinity and Horizontal Asymptotes