Jillian Holbrook
Jillian Holbrook
AP Calculus AB/BC ♾️
279 resourcesSee Units
What is Implicit Differentiation?
🎥Watch: AP Calculus AB/BC - Implicit Derivatives
Back in pre-calculus, you likely learned or talked about how there are two different types of equations: explicit equations and implicit equations.
An explicit equation is written such that y is isolated on one side. For example, y=2x+3 is an explicit equation. We know that for each value of x, there will only be one value of y.
Implicit equations are not as straightforward. Most of the time, an implicit equation will have x and y on the same side. So if x and y are on the same side, how can we differentiate an implicit equation?
How to Differentiate Implicitly
First off, let’s review the notations we can use for derivatives:
.png?alt=media&token=467543be-5b3a-4cd7-ac3f-3d291e0bf461)
Implicit Differentiation does not use the f’(x) notation. Instead, we will use the dy/dx and y' notations.
There are three main steps to successfully differentiate an equation implicitly.
- Get the y’s isolated on one side
- Factor out y’
- Isolate y’
Let’s look at an example to apply these steps.
.png?alt=media&token=4390de53-e542-4ccd-92fb-2dcbd4f20d5c)
Implicit Differentiation Practice
You’ll be a pro at implicitly differentiating in no time! Try the practice problems below and check them when you’re finished in the corresponding section at the end of this guide.
.png?alt=media&token=28754308-41fd-40e9-aa52-1dc3a537c4bb)
Answers
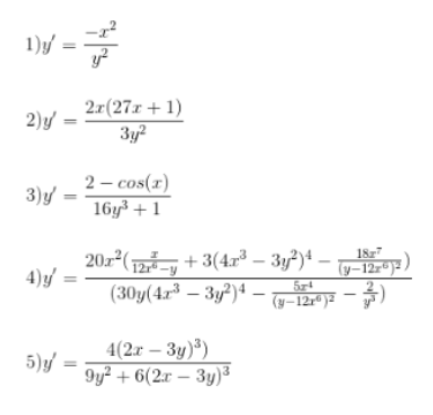
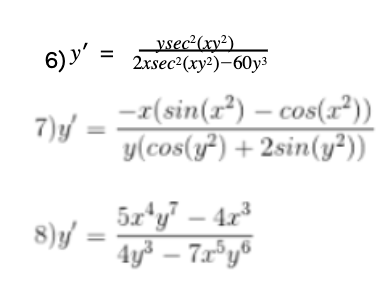
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
🧐Multiple Choice Questions (MCQ)
✍️Free Response Questions (FRQ)
📆Big Reviews: Finals & Exam Prep

© 2023 Fiveable Inc. All rights reserved.