📚

All Subjects

⚙️

AP Physics C: Mech

🚀

Unit 2

2.2 Circular Motion

7 min read•january 18, 2023

Gerardo Rafael Bote

Daniella Garcia-Loos

Gerardo Rafael Bote

Daniella Garcia-Loos

AP Physics C: Mechanics ⚙️

68 resources

See Units

Circular Motion

Before talking about Newton's third law, it's very important that we look at how circular motion is affected in accordance with Newton's first 2 laws. For right now, let's look at how UCM (Uniform Circular Motion) works. Also known as Centripetal Motion, Uniform Circular Motion refers to objects moving in a circular path with constant speed.

Uniform circular motion refers to the motion of an object moving in a circular path at a constant speed. Here are some key things to remember about UCM:

The object's velocity is always tangent to the circle, meaning it is constantly changing direction.
The acceleration of the object is always towards the center of the circle, known as centripetal acceleration.
This acceleration is caused by a force, known as the centripetal force, acting on the object towards the center of the circle.
The strength of the centripetal force is determined by the mass of the object, the radius of the circle, and the speed of the object.
The period of the motion, or the time it takes to complete one full revolution, is determined by the radius and speed of the object.
Uniform circular motion can be observed in various real-world situations, such as planets orbiting a star or a car turning a corner on a road.

First:

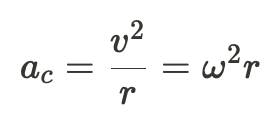
Therefore,

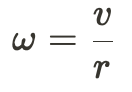
a_c stands for centripetal acceleration, meaning that there is a ΣF=ma_c relationship in the circular path.

Ω stands for angular velocity, v is the tangential velocity, and r is the radius.

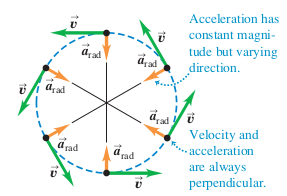
Image from Physics Stack Exchange

You need to differentiate how the different vectors of motion work in a circular path:

a_c is ALWAYS pointed toward the center of the circle.

Therefore, F_c (centripetal force) is also pointed toward the center of the circle.

Tangential velocity (v_t) is directed along with the direction the mass is going in (clockwise or counterclockwise) AND is perpendicular with a_c.

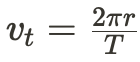
where T is the period and r is the radius.

The magnitude of velocity does not change but the direction does, which results in constant acceleration!

You can also rewrite Newton's second law to accommodate circular motion:

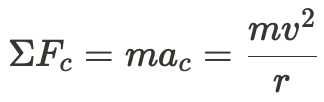
There is also tangential acceleration (a_t) within an object's circular motion (This might be useful when learning Non-UCM):

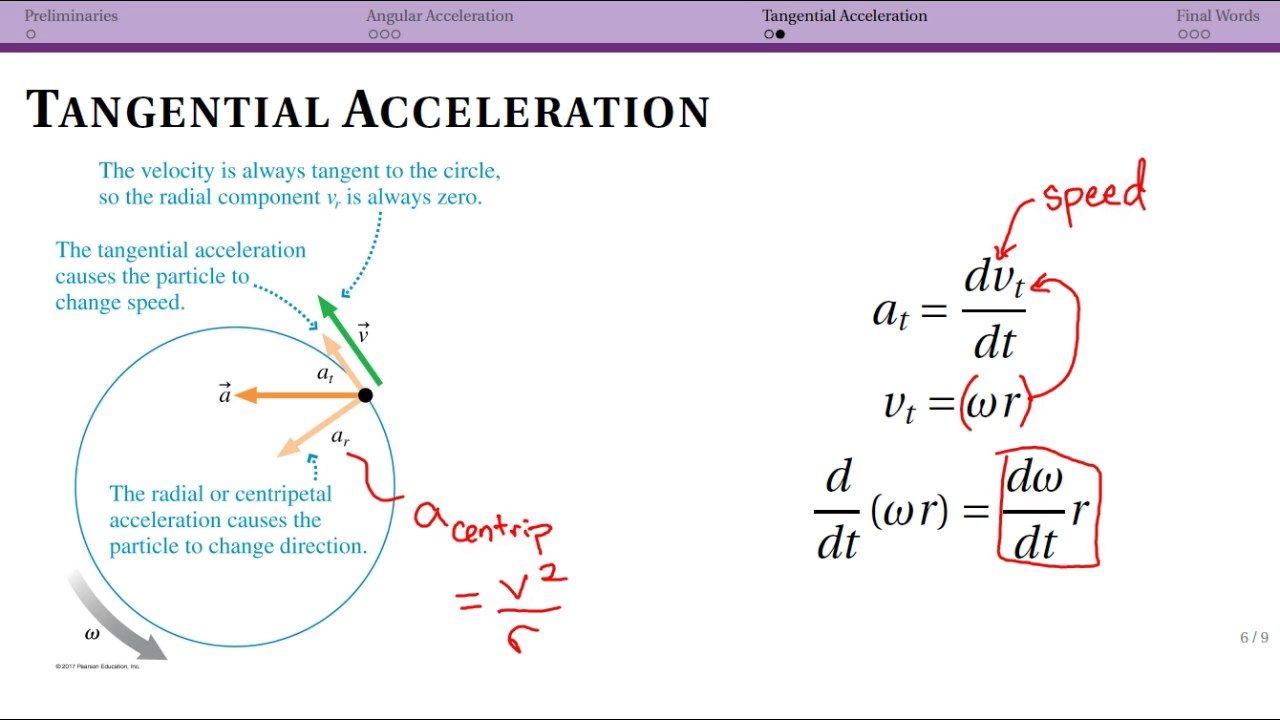
Image taken from ASCPhysicsAndAstronomy YouTube Video: Non-uniform Circular Motion: Tangential accel and summary

To figure out the object's overall acceleration in a circular path, apply Pythagoras' Theorem to both centripetal and tangential acceleration:

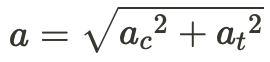
Here are key differences between tangential and angular velocities:

Tangential velocity refers to the velocity of an object moving in a circular path that is tangent to the circle of motion. It is a vector quantity and is measured in units of distance per time (e.g. m/s).

Angular velocity refers to the rate at which an object is rotating around a central point. It is measured in units of angle per time (e.g. radians per second).
The relationship between tangential velocity and angular velocity can be described by the equation: tangential velocity = angular velocity x radius.
Tangential velocity is an instantaneous measure of an object's speed at a specific point in its circular path, while angular velocity is a measure of how quickly the object is rotating overall.
Changes in tangential velocity can be caused by changes in speed or direction of motion, while changes in angular velocity can be caused by changes in rotation rate or direction of rotation.
An object can have a constant tangential velocity but changing angular velocity, for example when it is moving on a circular path but also spinning around its own axis.
Additionally, an object can have a constant angular velocity but changing tangential velocity, for example when it is spinning on its own axis but also moving in a circular path.

Vertical Circles

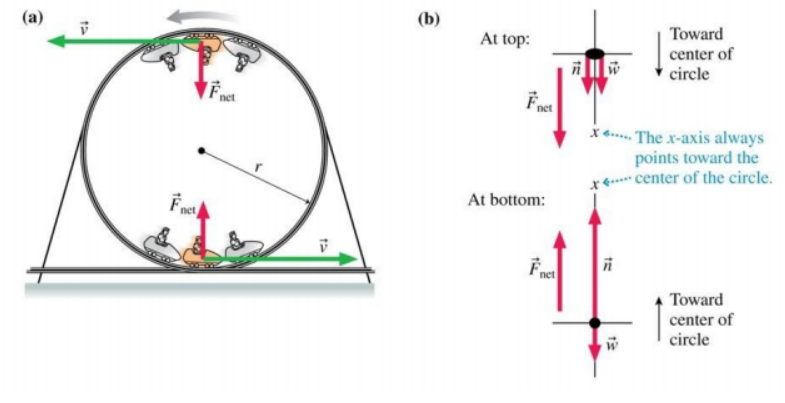
Image from Physics for Scientists and Engineers: A Strategic Approach Lecture (Shared by Miami University)

Vertical circles/loops are a popular scenario when discussing centripetal motion. AP loves to ask questions about critical speed/velocity in these problems. Critical speed occurs when the only centripetal force acting on the object is caused by gravity and is usually the minimum speed at the top of the vertical loop.

On another note, the maximum speed of a vertical loop is typically at the bottom of the circle. Be prepared to combine these scenarios with energy concepts in the future!

As you see in part (b) above, the FBDs of the roller coaster are different at the top of the loop and at the bottom. Normal force (or tension, if the object is attached to a rope/string) plays a big role in how the FBDs are constructed. AP loves to ask if you can figure out the value (or at least, the expression) that the normal force is equal to. Be careful about how to apply Newton's 2nd Law here. This is how you should set up your work to demonstrate your understanding of how vertical loops work.

Since we're dealing with circular motion, you need to consider what is considered a positive or negative vector. In circular motion, the vector is usually positive if it points toward the center, and the vector is usually negative if it points away from the center.

To figure out how to solve for F_n (normal force), look at the work below. (Remember, writing the equation below will likely give you 1-2 points!)

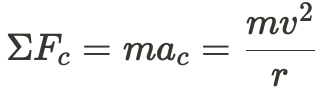
This is likely how you would set up the equation if the object was at the top of the loop:

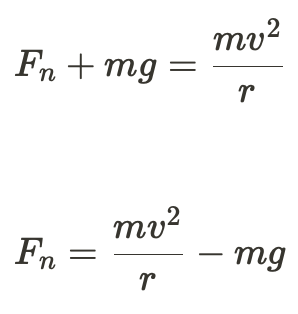
You can also figure out the amount of kinetic friction force the loop at the top is giving off by using

as shown below:

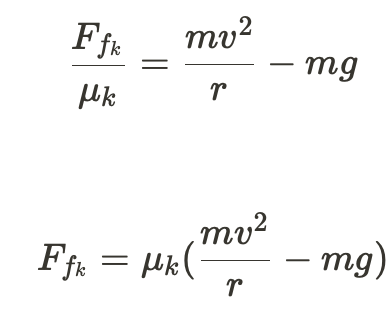
On the other hand, this is likely how you would set up the equation if the object was at the bottom of the loop:

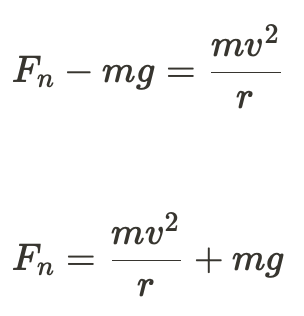
Again, you can also figure out the amount of kinetic friction force the loop is giving off at the bottom using

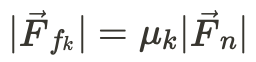
as shown below:

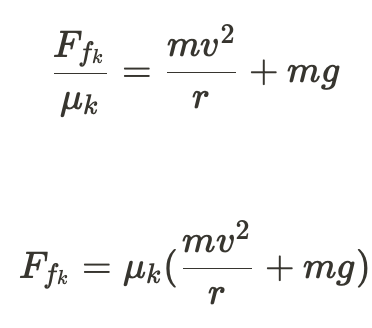
Banked Curves

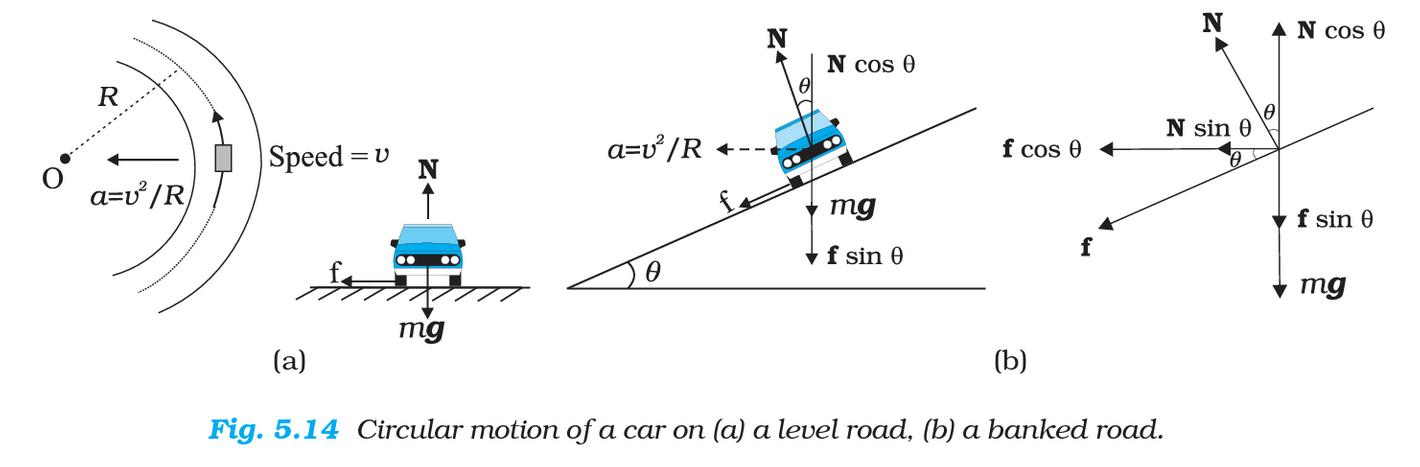
Image from Physics Stack Exchange

Banked curves are another situation that is seen a lot in relation to centripetal motion. AP also loves to ask questions about the minimum and maximum speeds of objects on banked curves/surfaces that have friction. As you can see from the figure, Normal force and (static) Friction force are parts of the centripetal force. Normal force is what keeps your car on the road in these banked curves!

A banked curve is a type of road or track design that includes a slope or incline on the outer edge of a curve.

The purpose of a banked curve is to provide an additional force, known as the centrifugal force, that helps keep vehicles on the road or track while turning.

Centrifugal force is an apparent force that acts in the opposite direction of the center of rotation, and its strength depends on the speed and radius of the turn.

To solve a problem with a banked curve, the following information is needed:

The coefficient of friction between the tires of the vehicle and the road surface is an important factor to determine the necessary angle of inclination of the banked curve.

To calculate the minimum speed required to keep a vehicle from sliding out of the curve, you can use the formula: v² = r * g * cos(theta)

To calculate the minimum angle of inclination required for a given speed and radius, you can use the formula: theta = arctan(v² / (r * g)) Where v is the speed of the vehicle, r is the radius of the curve, g is the gravitational acceleration, and theta is the angle of inclination of the banked curve

Practice Questions:

Image from Varsity Tutors

Answer

This problem deals centripetal force because we have to figure out how much velocity we need to maintain to make sure that the tension within the rope does not exceed the magnitude of T_{max}. Since we are also dealing with centripetal force, you might as well apply Newton's 2nd Law (circular form) here:

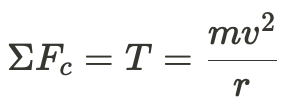
⚠️Wait... isn't there supposed to be a mg part in the equation above? No, read the question again; since we are looking at the circular path from a point of view above, it can be assumed that gravity is not directly affecting the centripetal force of the ball. (tl;dr: This is not a vertical loop.)

Since we want the rope to not break, it should be clear that the tension in the rope should never exceed T_{max}:

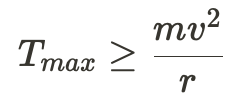
(Again, writing the equation above will likely get you points on the AP Exam!)

Finally, solve for velocity:

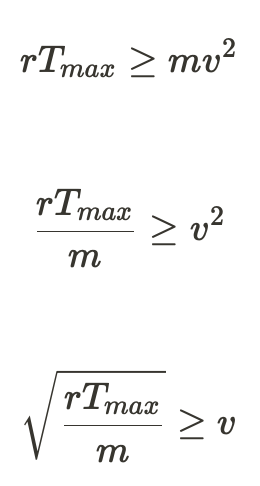
Answer

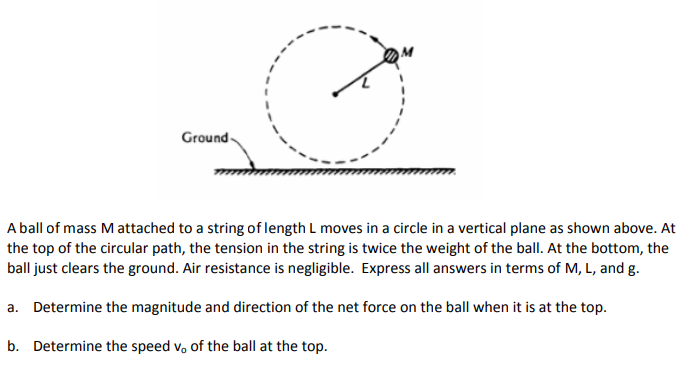
Since we are dealing with centripetal force, you should always know that the direction of the centripetal force is always pointing toward the center of the circle. In this case, when the ball is at the top of the circular path (vertical loop), the direction of the net force is pointing downward. To calculate the magnitude of the net force, you need to read the problem: "The tension in the string is twice the weight of the ball." Knowing this, you can write that T=2W=2mgT=2W=2mg, where WW represents the weight of the ball, mm represents the mass of the ball, and gg represents the acceleration due to gravity. Now just apply Newton's 2nd Law for the ball at the top of the loop:

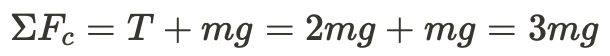
This is where you should expand the net force equation above to answer part (b). Now you can say:

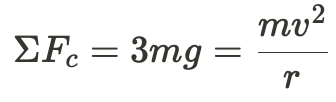
You know that r = L, so you replace as follows:

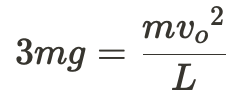
Then, solve for v_o.

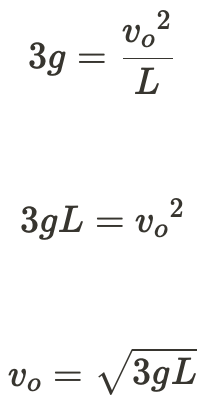
What is the radius of a bobsled turn banked at 75.0° and taken at 30.0 m/s, assuming it is ideally banked? (Taken from Lumen Learning)

Answer

First, start off by drawing a Free Body Diagram for the bobsled on the banked curve. Then we can write our equations for the X and Y components of the forces at work on the bobsled.

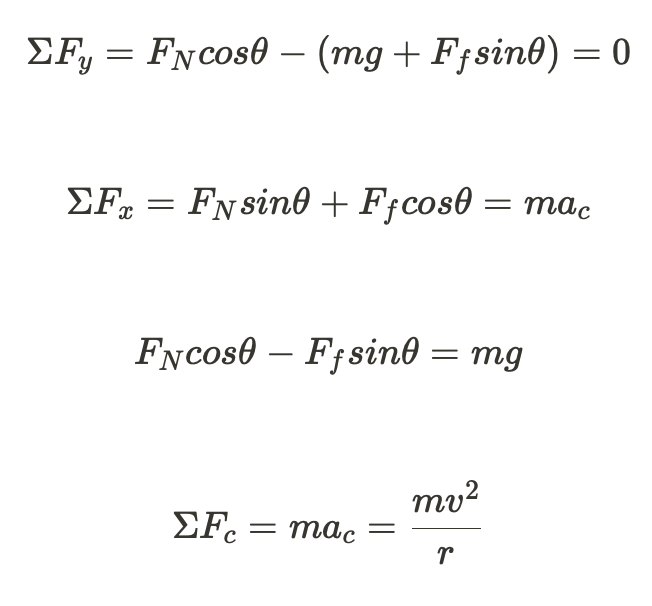
The forces in the X direction are the centripetal forces, therefore:

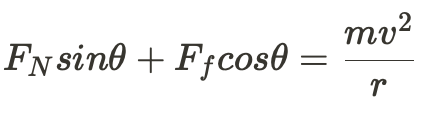
We need to get rid of the normal force and the friction force in order to only have variables we know or are searching for.

Remember that:

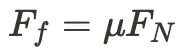
By solving the system of equations we get:

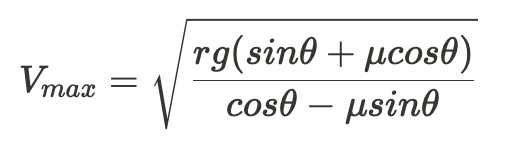
When we assume the curve is ideally banked, we assume that there is no friction between the sled and the ground, so we can cancel out the friction related terms.